오늘은 트리(Tree)의 개념에 대해서 알아보겠습니다.
트리의 개념 / 용어
트리는 노드로 이루어진 계층적 관계를 표현하는 비선형 자료구조입니다.
나뭇가지 형태의 이미지를 나타내며 트리 관련 용어를 먼저 살펴보도록 합시다.

위 트리를 보고 용어 설명 먼저드리도록 하겠습니다.
노드(Node) : 위 트리그림의 a,b,c,d,e,f 들을 노드라 합니다.
간선(Edge) : 노드와 노드를 연결하는 선을 간선이라고 합니다.
부모노드(Parent node) : 자식노드가 있는 노드 ( 예시 : b, c )
자식노드(Child node) : 부모노드로 부터 나온 노드 ( 예시 : d, e, f )
(예시 : 부모가 a이면 자식은 b,c / 부모가 b이면 자식은 d,e )
루트노드 (Root node) : 부모(Parent)가 없는 노드로 모든 트리는 단 하나의 루트 노드를 가집니다. (예시 : a )
단말노드 (Leaf node) : 자식이 없는 노드로 터미널(terminal)노드라고도 한다. (예시 : d, e, f)
노드의 깊이(depth) : 루트 노드에서 특정 노드에 도달하기까지 거쳐야 하는 간선의 수 (예시 : d의 깊이 : 2 / b의 깊이 : 1)
노드의 차수(degree) : 자식 노드의 개수 (예시 : b의 차수 : 2 / c의 차수 : 1)
트리의 차수 : 트리의 최대 차수로 보통 2
트리의 특징
- 트리의 루트노드는 하나이다.
- 루트노드는 0개 이상의 자식 노드를 갖는다.
- 트리에는 사이클 및 루프가 존재할 수 없다. (시작 노드에서 출발해 다시 돌아올 수 있으면 사이클이 존재한다고 함)

트리의 종류
트리의 종류에는 이진트리, 편향 이진트리, 완전 이진트리, 전 이진트리, 포화 이진트리가 있다.
이진트리 (Binary Tree)
이진트리는 각 노드가 최대 두 개의 자식을 갖는 트리를 의미한다.
각 노드는 자식이 0개, 1개, 2개가 있을 수 있다.

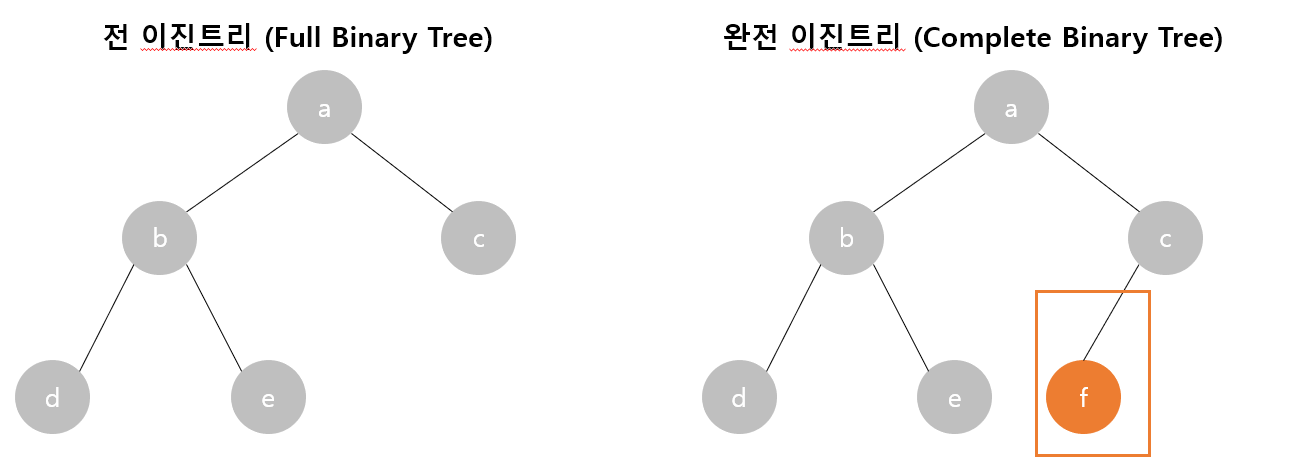
완전 이진트리 (Complete Binary Tree)
마지막 레벨 제외 그 이전 레벨까지는 모든 레벨이 채워져 있어야 하며, 노드는 왼쪽에서 오른쪽으로 채워져야 한다.

전 이진트리 (Full Binary Tree)
전 이진트리는 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리로 1개의 노드를 갖는 트리는 없어야 한다.

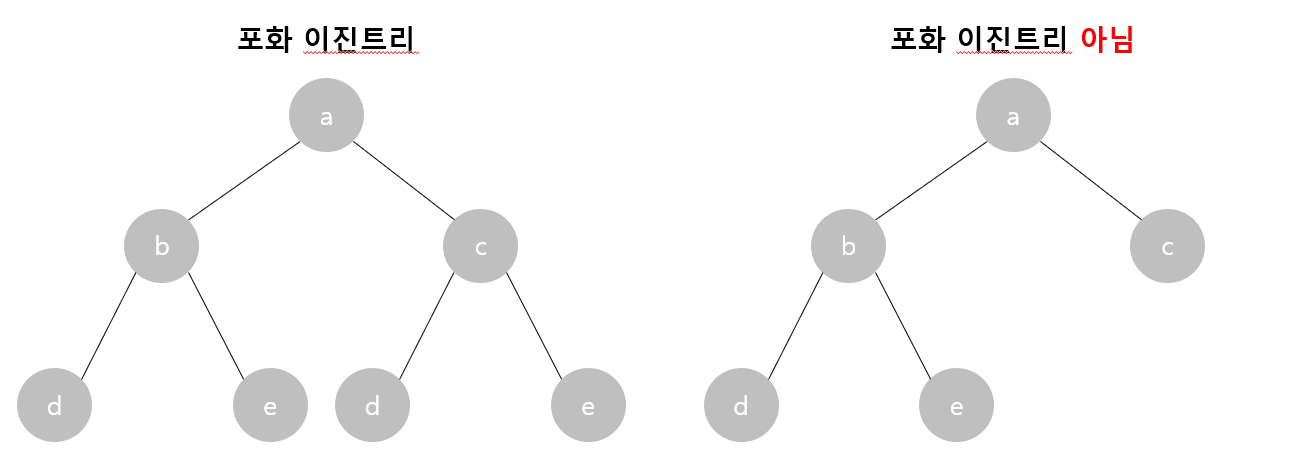
포화 이진트리 (Perfect Binary Tree)
포화 이진트리는 모든 레벨이 (마지막 레벨까지도) 노드로 꽉 차 있는 트리이다.
모든 말단 노드가 동일한 깊이를 가지는 트리이다.
트리의 종류가 많아 외우기에 좀 헷갈릴 수 있는 부분이 있다.
포화 이진트리는 의미 그대로 꽉 차있는 트리이기 때문에 모든 노드가 다 채워져있다고 보면 된다.
완전 이진트리와 전 이진트리가 헷갈릴 수 있는 부분인데 이렇게 외우고 다니면 좀 덜 헷갈리는 것 같습니다.
완전 이진트리는 전 이진트리보다 한글자가 더 있기 때문에 한 노드가 더 있어도 된다고 생각하면 헷갈리지 않을 수 있다고 봅니다.
감사합니다.
'IT 이것저것' 카테고리의 다른 글
| [네트워크] 로드밸런싱(Load Balancing)이란? 종류와 기법 (2) | 2023.01.25 |
|---|---|
| 이진탐색트리(Binary Search Tree) 설명 및 특징 (2) | 2023.01.24 |
| [저장소] RAID의 개념, 목적 및 종류(RAID LEVEL) (5) | 2023.01.23 |
| [인프라] 스케일 업(Scale-up) 과 스케일 아웃(Scale-out) 비교 (2) | 2023.01.20 |
| Failover 란 무엇인가? 개념 및 설명 (4) | 2023.01.18 |




댓글