저번시간에는 이진트리의 개념 및 설명, 종류에 대해 알아보았고
이번에는 이진탐색트리(Binary Search Tree) 에 대해 알아보도록 하겠다.
이진탐색트리란 이진 트리 구조를 나타내는데 다음과 같은 특징이 있습니다.
이진 탐색 트리의 특징
- 각 노드에 값이 있다.
- 루트노드의 왼쪽 서브 트리에는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다.
- 루트노드의 오른쪽 서브 트리에는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다.
- 좌우의 서브 트리들도 각각 이진 탐색 트리이다. (재귀함수 or 프랙탈 구조)
- 트리의 높이(레벨)가 h라면 시간 복잡도는 O(h) 이다.

이진 탐색 트리의 탐색과정
이진 탐색 트리의 탐색과정은 다음과 같다.
(1) 루트 노드의 키와 찾고자 하는 값을 비교한다.
(2) 찾고자 하는 값이 루트 노드의 키보다 작으면 왼쪽 서브 트리를 탐색한다.
(3) 찾고자 하는 값이 루트 노드의 키보다 크면 오른쪽 서브 트리를 탐색한다.
탐색을 하다가 값을 찾으면 탐색과정은 종료된다.

위 트리에서 7을 찾으려고 했을 때, 먼저 루트 노드인 6과 비교를 한다.
6과 비교를 했을 때 7이 더 크므로 6의 오른쪽 서브트리로 넘어가고
오른쪽 서브트리의 노드인 8과 비교를 하게 되는데 8과 비교 했을 시 8보다는 7이 작으므로
8의 왼쪽 서브트리를 탐색하게 된다.
8의 왼쪽 서브트리에서 탐색을 하게 될 때 7을 찾았으므로 탐색은 종료된다.
위 트리의 높이(h)는 2이므로, 탐색과정은 2번 이하의 탐색이 이루어진다.
즉, 이진 탐색 트리를 탐색할 시 이진 탐색 트리의 높이(h) 이하의 탐색이 이루어 진다.
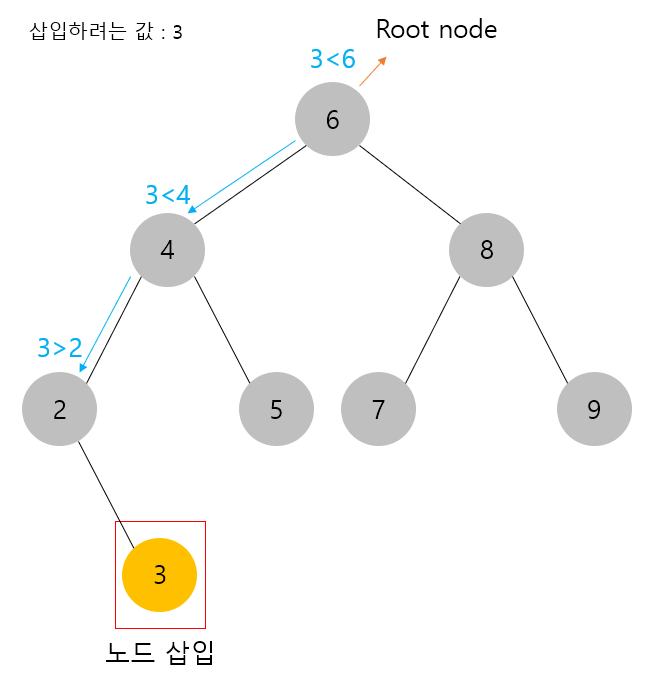
이진 탐색 트리 값 삽입 (Insert)
이진 탐색 트리에 값을 삽입하게 될 경우가 있는데 해당 경우의 탐색과정을 살펴보자.
(1) 삽입할 값을 루트 노드와 비교한다.
(2) 삽입할 값이 루트 노드와 값이 같으면 중복 값 (key)를 허용하지 않기 때문에 오류를 발생시킨다.
(3) 삽입할 값이 루트 노드의 키보다 작으면 왼쪽 서브 트리를 탐색하여 해당 서브트리에 공간이 있으면 삽입하고, 비어있지 않다면 다시 탐색을 진행한다.
(4) 삽입할 값이 루트 노드의 키보다 크면 오른쪽 서브 트리를 탐색하여 해당 서브트리에 공간이 있으면 삽입하고, 비어있지 않다면 다시 탐색을 진행한다.
이진 탐색 트리 값 삭제 (Delete)
이진 탐색 트리에 값을 삭제하게 될 경우가 있는데 해당 경우의 상황을 나누어서 생각해보자.
일단 삭제하려는 값을 탐색해가는 과정은 이진 탐색 트리 탐색과정으로 진행한다.
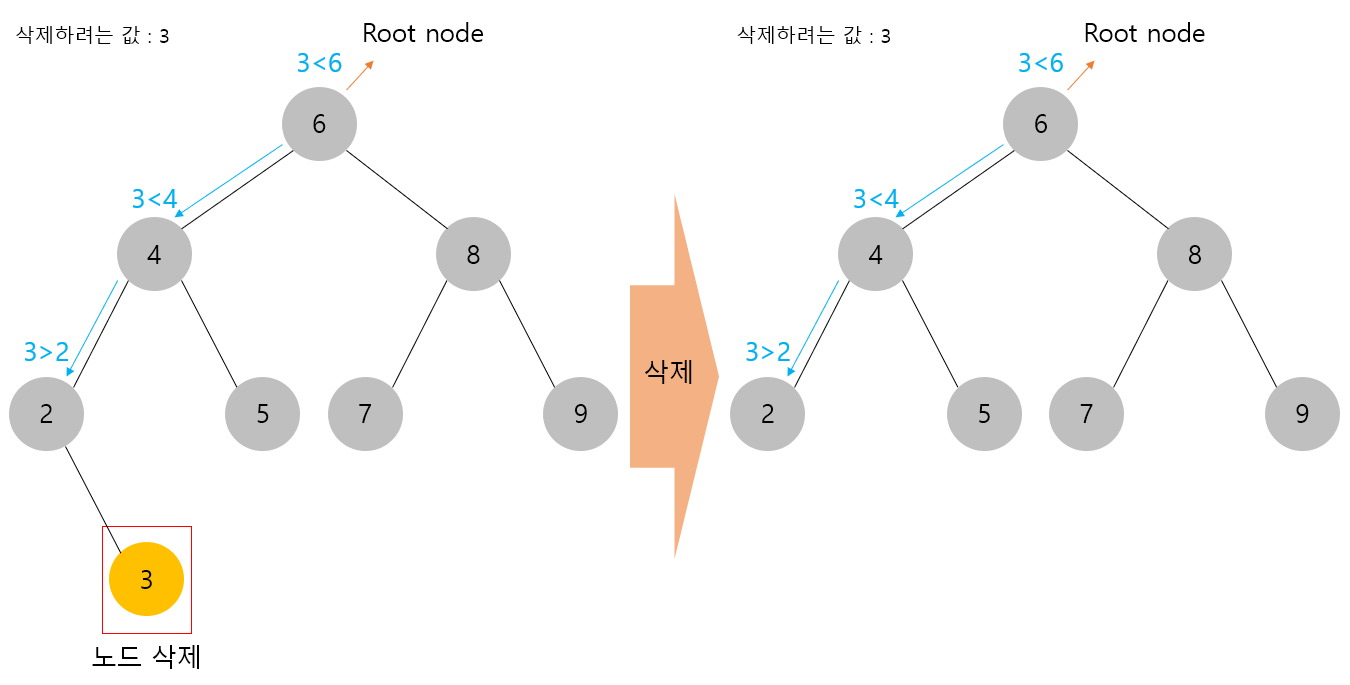
(1) 삭제하려는 노드가 단말 노드인 경우
삭제하려는 노드가 단말 노드인 경우는 굉장히 간단하다.
이진 탐색 트리의 구조를 바꿀 필요 없이 해당 단말 노드만 삭제해주면 된다.
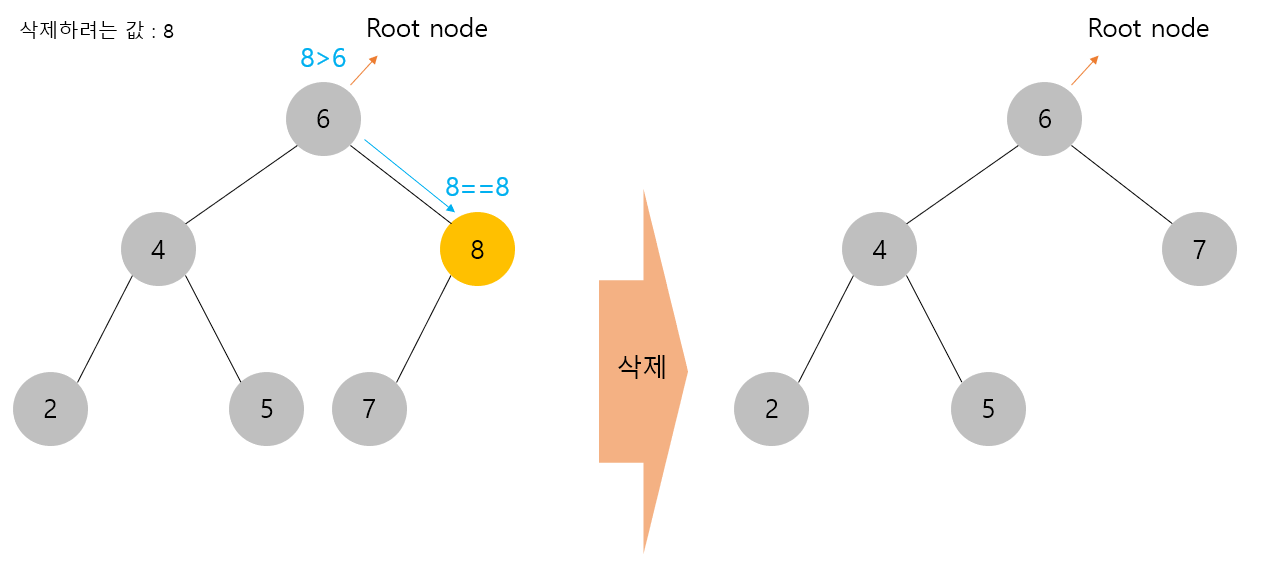
(2) 삭제하려는 노드의 서브 트리가 한개인 경우
아래와 같이 값이 8인 노드를 삭제하려고 할 때,
그 8에 있는 서브트리가 하나인 경우에는 해당 서브트리를 삭제된 부모노드의 자리에 대체해준다.
(3) 삭제하려는 노드의 서브 트리가 두개인 경우
아래의 그림과 같이 서브 트리가 두 개인 루트노드(Root node)인 6을 삭제한다고 했을 때, 값이 6인 노드가 사라지면 그 밑의 서브트리 중에 어떤 값을 가진 노드로 대체할 것인지 판단해야 한다.
이 때 우리는 두 가지 방식을 사용할 수 있다.
a. 삭제된 노드의 왼쪽 서브 트리 중 가장 큰 값을 가진 노드로 대체하는 방식을 취한다.
b. 삭제된 노드의 오른쪽 서브 트리 중 가장 작은 값을 가진 노드로 대체하는 방식을 취한다.
아래 이미지는 a의 방식을 사용하여 삭제(delete)를 해보았다.
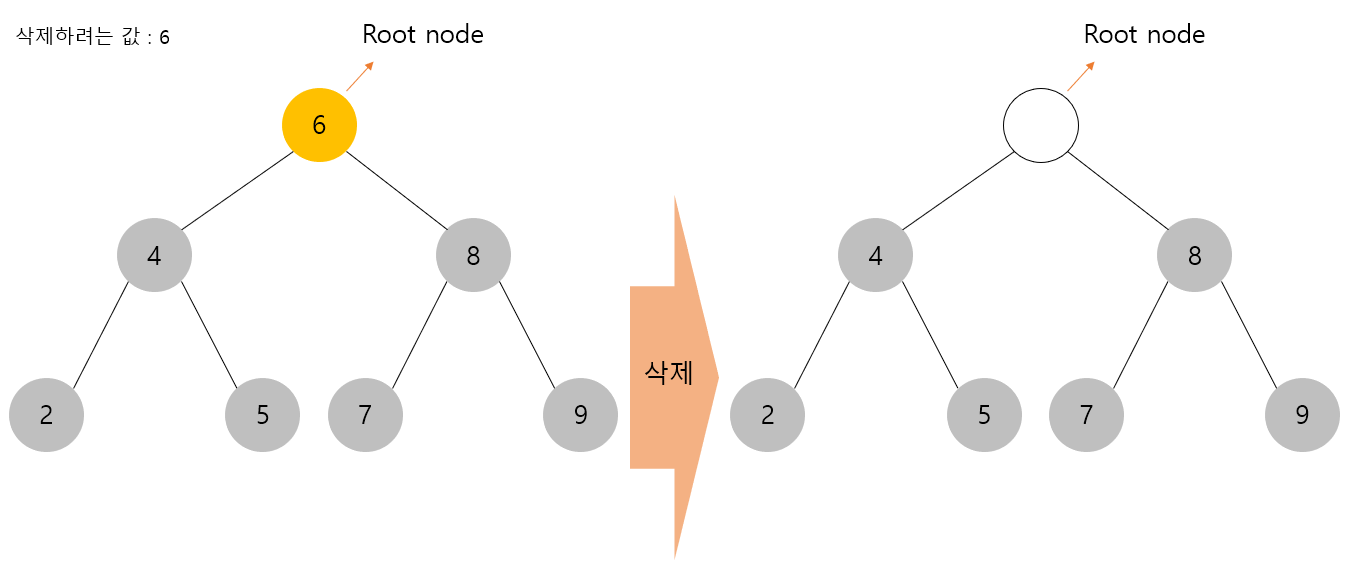
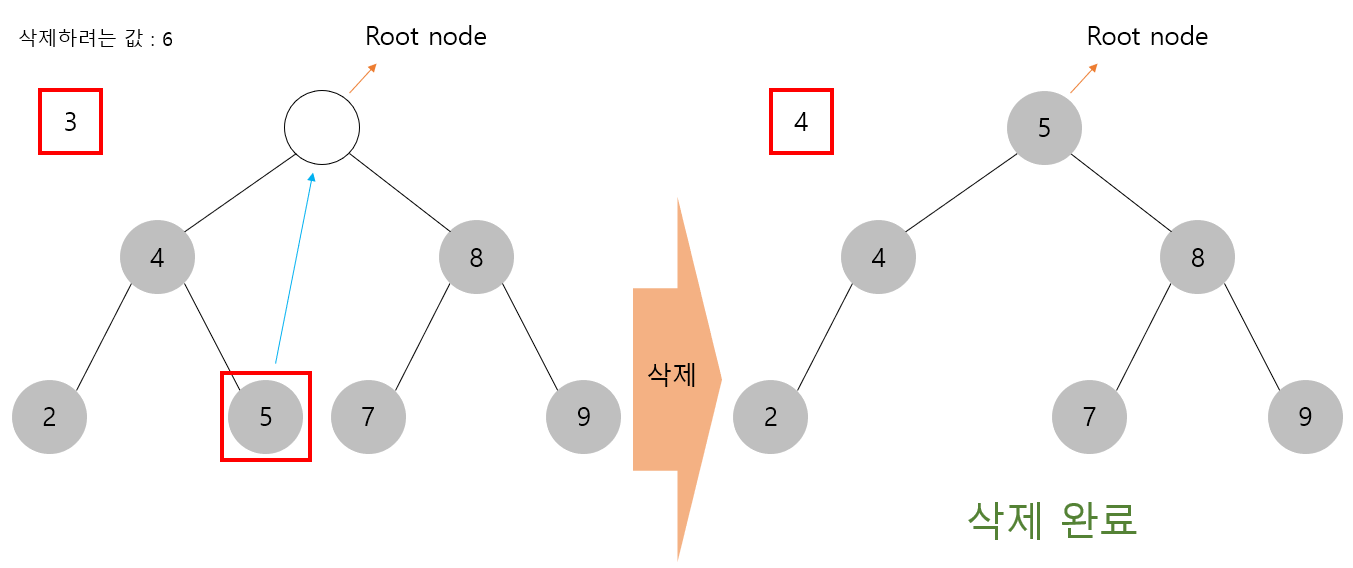
다음과 같이 값이 6인 노드는 삭제되었고 왼쪽 서브트리에서 가장 큰 값인 5가 해당 자리를 대체하였다.
만약 왼쪽 서브트리에 있던 값인 5 노드에 또 서브트리가 달려 있었다면 해당 서브트리도 이진탐색트리의 규칙에 의해 재배열해주면 되는 것이다.
이상으로 이진 탐색 트리의 개념 및 특징, 탐색 과정에 대해 알아보았다.
'IT 이것저것' 카테고리의 다른 글
| [인공지능] AGI란 무엇인가? AI의 발전과 ChatGPT의 등장 (0) | 2023.01.26 |
|---|---|
| [네트워크] 로드밸런싱(Load Balancing)이란? 종류와 기법 (2) | 2023.01.25 |
| 트리(Tree) 개념, 용어, 종류(완전 이진트리, 전 이진트리, 포화 이진트리) (4) | 2023.01.24 |
| [저장소] RAID의 개념, 목적 및 종류(RAID LEVEL) (5) | 2023.01.23 |
| [인프라] 스케일 업(Scale-up) 과 스케일 아웃(Scale-out) 비교 (2) | 2023.01.20 |




댓글